[学习笔记] 数学笔记丨整式与分式 ... ...（更新中）

一、数与式

1. 概念

●  代数式：有理式、无理式。

○  有理式：整式、分式。

○  无理式：带有根号且根号下含有字母的式子、无限不循环小数。

▸  注. 代数式内的分数必须简化为假分数。

2. 整式与分式

●  整式：单项式、多项式。

○  单项式：数与字母的积。

▸  注. 单独一个数或一个字母也是单项式。

○  单项式的系数：数。

○  单项式的次数：字母的指数之和。

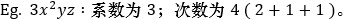
○  多项式：单项式的和。

▸  注. ① 单项式次数为几就叫几次项，不含字母叫常数项；② 多项式有几个单项式就叫几项式。

○  多项式的次数：次数最高的单项式的次数（字母的指数之和）。

○  多项式的排列：① 升幂，按某一个字母的指数从小到大的顺序排列；

○  单项式的排列：② 降幂，按某一个字母的指数从大到小的顺序排列。

▸  排列注意事项：① 符号；② 字母；③ 升降幂；④ 同类项。

▸  同类项：① 字母及其指数皆相同的单项式（与系数、排列顺序无关）；② 常数项。

●  整式的计算（运用分配律）

○  运算法则

○  平方差公式

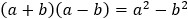
○  完全平方公式

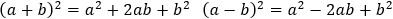
▸  注. 多项式被另一整式整除，后者即是前者的因式。

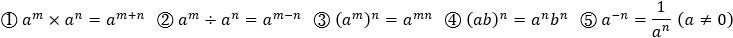
○  同底数幂相乘，底数不变，指数相加；同底数幂相除，底数不变，指数相减。

▸  0指数幂：任何不为0的数的0次幂，都等于1。

○  特殊概念

○  a、b 互为相反数。

○  a、b 互为倒数。

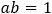
○  a、b 互为负倒数。

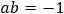
○  a 的绝对值等于 b。

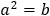
○  各单项式皆 ≥ 0，整式为 0，则各单项式为 0。

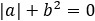
●  分式

○  分母为 0，则分式无意义。

▸  分式值为 0，则分子为 0 且分母不为 0。

○  分式方程：分母含有未知数的方程。

○  方程无解：解为增根；整式方程无解。

▸  增根，方程求解后得到的不满足题设条件的根。